LA PROPORCIÓN ÁUREA
| 1'6180339887498948482045868343 6563811772030917980576 28621354486227052604628189024 49707207204189391137484 7540880753868917521 2663386222353693 1793180060766 7263544333890865959 39582905638322 661319928 29026788 ......
No, no me he confundido, esto no es una entrada de Matemáticas. O tal vez si.
Ya veremos.
Voy a contaros la historia del número que puedes ver arriba, del que os he colocado
"unos cuantos" decimales y al que, para abreviar, vamos a llamar solo por sus tres primeros:
1'618
Este número recibe varios nombres:
número de oro, Proporción áurea o Divina proporción.
También se le conoce por la letra griega PHI
Φ
¿Pero que tiene que ver con el arte?
Bueno. El arte siempre ha buscado crear equilibrio y belleza. El arte griego,
por ejemplo estaba muy obsesionado con esa idea, y fue precisamente en la antigua Grecia donde se descubrió y utilizó este número para crearla.
¿Como?
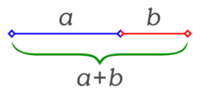
El número de oro expresa una proporción entre dos segmentos de una recta;
o sea, una construcción geométrica. Es una manera de dividir un segmento en dos.
La longitud total a+b es al segmento más largo a,
como a es al segmento más corto b.
Osea, que si divido lo que mide el total del segmento entre el trozo largo,
el resultado es el mismo que el de dividir el trozo largo entre el pequeño. Y lo mas curioso, ese resultado siempre es el número áureo, 1'618.
¡¡¡Pero que tiene que ver!!!
Vale, vale, Vamos despacio. mira esta imagen con
atención y elige el rectángulo que te parece mas
bonito y bien proporcionado.
Nota: Al final de la entrada te descubro cual es el que cumple la divina proporción.
Y ahora mira esta otra:
Un poco destrozado por el tiempo
pero uno de los edificios mas bellos de la historia.
Si se divide la base por la altura el resultado es....
PHI.
Todo en el esta diseñado según la proporción áurea.
En la figura se puede comprobar que AB/CD=
Hay más cocientes entre sus medidas que dan el número áureo, por ejemplo: AC/AD=
A este rectángulo se le denomina rectángulo áureo.
Hoy día es muy popular. Ejemplos de rectángulos áureos los podemos
encontrar en las tarjetas de crédito, en nuestro carnet de identidad y también en las cajetillas de tabaco.
Mira como se construye gráficamente a partir de un cuadrado (ABDC):
El rectángulo (AECF) es áureo.
Y el (BECF) también.
¡Pues tampoco es para tanto!
No pienses eso. Todavía no has visto nada.
Resulta que si continuamos construyendo cuadrados dentro de los rectángulos
se puede trazar una espiral que muchos llaman espiral áurea o Espiral de Durero, porque fue ese artista del renacimiento quien la descubrió.
Podemos encontrar esta espiral en diversas figuras de la naturaleza
(plantas, galaxias espirales, ), así como en el arte.
¡Si te parece curioso
verás que aun no se han acabado las curiosidades!
HA LLEGADO EL MOMENTO DE HABLAR
DE LA REPRODUCCIÓN DE LOS CONEJOS.
¿No!, no me he vuelto loco.
En el siglo XIII, un matemático italiano llamado Leonardo de Pisa,
también conocido como Fibonacci, quería solucionar un
problema de la cría de conejos: ¿CUANTOS PARES TENDREMOS
AL CABO DE UN AÑO A PARTIR DE UNA SOLA PAREJA?
Fíjate:
Así se forma una sucesión infinita de números donde cada uno es la suma de los dos anteriores, llamada sucesión de Fibonacci:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...
Y qué ???
Pues resulta que en una espiral áurea, el lado de los cuadrados que la forman siguen esta progresión:
Sorprendente, ¿no?
Ahora mira estos vídeos. Te enseñarán mas cosas.
El primero en explicar va a ser el pato Donald. (empezamos suave) El siguiente es mas sesudo. un fragmento del programa redes.
Un pequeño fragmento que explica la belleza de uno de los lugares mas
hermosos del mundo:
Y ahora algo que interesa a mucha gente.
Bueno, espero que os haya gustado o interesado. Para finalizar, podéis entreteneros buscando proporciones áureas con la ayuda de un compás parecido al que habéis visto en el vídeo anterior. Encontrareis un pdf para imprimir en la caja de box. Y también un par de sesudos libros para usuarios avanzados. |
Por cierto, el rectángulo áureo es el segundo por la derecha de la fila de abajo.